深度残差网络(ResNet)中的残差块与恒等映射原理
1. 问题背景
在深度神经网络训练中,随着网络层数增加,模型容易出现退化问题(Degradation Problem):层数加深时,训练误差反而比浅层网络更大。这不是过拟合(因为训练误差也上升),而是由于梯度消失/爆炸或优化困难导致。ResNet通过引入残差块(Residual Block)解决了这一问题。
2. 残差块的核心思想
假设我们希望堆叠多个非线性层来拟合一个目标函数 \(H(x)\)(例如图像分类中的映射)。传统网络直接学习 \(H(x)\),而ResNet改为学习残差函数 \(F(x) = H(x) - x\),这样原函数变为 \(H(x) = F(x) + x\)。
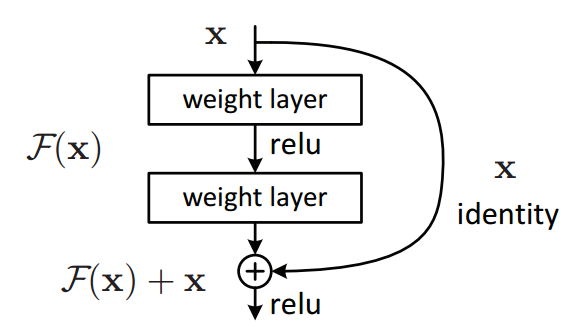
- 关键结构:在层之间添加跨层连接(Skip Connection),将输入 \(x\) 直接加到输出上(见图1)。
传统层:输出 = F(x)
残差块:输出 = F(x) + x
3. 为什么残差结构有效?
(1)梯度传播优化
假设网络第 \(L\) 层的输出为 \(y_L\),损失函数为 \(\mathcal{L}\)。根据链式法则,反向传播时梯度需从 \(y_L\) 传回第 \(l\) 层的输入 \(x_l\):
\[\frac{\partial \mathcal{L}}{\partial x_l} = \frac{\partial \mathcal{L}}{\partial x_L} \cdot \prod_{i=l}^{L-1} \frac{\partial y_{i+1}}{\partial y_i} \]
传统深层网络中,连乘可能导致梯度消失(梯度趋近0)或爆炸(梯度极大)。
在残差块中,第 \(l+1\) 层的输出为:
\[y_{l+1} = F(x_l) + x_l \]
对 \(x_l\) 求导:
\[\frac{\partial y_{l+1}}{\partial x_l} = \frac{\partial F(x_l)}{\partial x_l} + I \]
梯度变为 原梯度 + 1,即使 \(\frac{\partial F(x_l)}{\partial x_l}\) 很小,梯度仍能保持至少为1,缓解梯度消失。
(2)恒等映射的默认行为
如果某层的作用是冗余的(即理想映射 \(H(x) = x\)),传统网络需学习 \(F(x) = 0\)(非零权重拟合恒等映射较难),而残差块只需将 \(F(x)\) 的权重推向0即可实现 \(H(x) = x\),这比学习非零映射更容易。
4. 残差块的两种具体结构
ResNet根据网络深度设计了两种残差块:
(1)基本残差块(用于ResNet-18/34)
- 两层卷积:3×3卷积 → BN → ReLU → 3×3卷积 → BN
- Skip Connection:直接相加(要求输入输出维度相同)。
- 若维度不同,需在Skip Connection中加入1×1卷积调整维度(称为Projection Shortcut)。
(2)瓶颈残差块(用于ResNet-50/101/152)
- 三层卷积:1×1卷积(降维)→ 3×3卷积 → 1×1卷积(升维)
- 目的:减少参数量,提升计算效率(类似Inception模块)。
5. 残差网络的实际效果
- 在ImageNet数据集上,ResNet-152(层数>100)比VGG-16(层数=16)错误率显著降低。
- 退化问题被解决:深层网络的训练误差始终低于浅层网络。
- 后续变体(如Pre-activation ResNet)进一步优化了训练稳定性。
6. 总结
- 核心创新:通过跨层连接引入残差学习,将问题从学习 \(H(x)\) 转为学习 \(F(x) = H(x) - x\)。
- 优势:梯度传播更顺畅,缓解梯度消失;恒等映射更容易实现;支持极深网络设计。
- 应用影响:ResNet成为计算机视觉领域的基石结构,启发了DenseNet、Transformer中的残差连接等后续工作。
